Definition

The diameter of a tree is defined as follows:

• For any two vertices u and v in a tree, there is always exactly one simple path between them. The length of this simple path is referred to as the distance between vertices u and v.
• Given a vertex u in a tree and any other vertex v, the maximum distance between u and v is called the eccentricity of vertex u.
• The minimum eccentricity among all vertices in the tree is known as the radius of the tree, while the maximum eccentricity is referred to as the diameter of the tree.

Proof

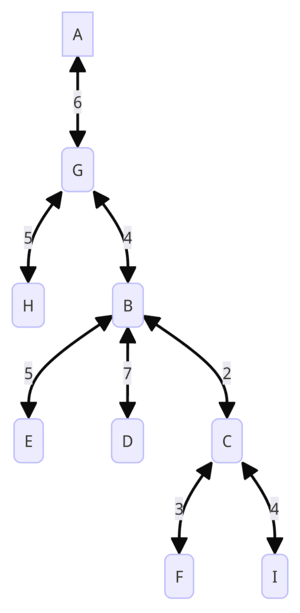
In a given tree, the diameter is defined as 17, and the radius is defined as 10.

The simplest method to find the diameter of a tree is as follows:

Select any vertex in the tree and find the vertex u that is the furthest away from it. If there are multiple furthest vertices, select any one of them.
From vertex u, find the vertex v that is the furthest away. The diameter of the tree is the distance between vertex u and v.
This method is based on the fact that there always exists a diameter of the tree that has one endpoint being the vertex furthest from an arbitrary vertex. This fact can be proven as follows:

Proof:

Assume that for some vertex p, one of the furthest vertices from it is u, and there exists no diameter of the tree with u as one endpoint.

Since the diameter of a tree is the length of the longest path between any two vertices, let's denote these two vertices as (v₁) and (v₂). Also, let's denote the vertex on the simple path between (v₁) and (v₂) that is closest to u as a, and the vertex on the simple path between p and u that is closest to a as b.

Let the distance between vertex (x) and vertex (y) be denoted as (d(x,y)). Therefore, the diameter of the tree can be expressed as (d(v₁,v₂)). According to 2, (d(v₁,v₂) = d(v₁,a) + d(a,v₂)) and (d(p,u) = d(p,b) + d(b,u)).

Since u is one of the furthest vertices from p, (d(p,u) ≥ d(p,v₁)). Also, (d(p,v₁) = d(p,b) + d(b,a) + d(a,v₁)).

From 3 and 4, (d(p,b) + d(b,u) ≥ d(p,b) + d(b,a) + d(a,v₁)), and subtracting (d(p,b)) from both sides gives (d(b,u) ≥ d(b,a) + d(a,v₁)).

Adding (d(b,a)) to both sides of the last equation from 5, (d(b,u) + d(b,a) ≥ 2d(b,a) + d(a,v₁)), and since (d(b,a) ≥ 0), (d(b,u) + d(b,a) ≥ d(a,v₁)).

Since the simple path between b and u, and the simple path between b and a do not share any edges, (d(b,u) + d(b,a) = d(a,u)). Therefore, (d(a,u) ≥ d(a,v₁)), and adding (d(a,v₂)) to both sides gives (d(a,u) + d(a,v₁) ≥ d(v₁,v₂)).

Since the simple path between a and u, and the simple path between a and (v₁) do not share any edges, (d(a,u) + d(a,v₁) = d(v₁,u)). Therefore, (d(v₁,u) ≥ d(v₁,v₂)).

Assuming (d(v₁,v₂)) as the diameter of the tree, (d(v₁,u) ≤ d(v₁,v₂)).

From 8 and 9, (d(v₁,u) = d(v₁,v₂)), which means the distance between u and (v₁) is equal to the diameter of the tree, thus contradicting the assumption in 1. Therefore, the assumption in 1 is proven to be incorrect.

So, the diameter of a tree can be determined with just two BFS or DFS traversals. However, if some edge weights are negative, one or both ends of the tree's diameter may not be a leaf node. In such cases, the previous method fails to calculate the diameter, but it can be determined using Dynamic Programming.

Example

Problem
The diameter of a tree is the longest distance between any two nodes in the tree. Write a program to find the diameter of a tree.

Input
The tree is given as input. First, the number of vertices V in the tree is given (2 ≤ V ≤ 100,000). Then, starting from the second line, the information about the edges is given for V lines. The vertex numbers are assigned from 1 to V.

First, a vertex number is given, followed by pairs of integers representing the connected edges. Each pair consists of a vertex number and the distance to that vertex. For example, the fourth line might show that vertex 3 is connected to vertex 1 with a distance of 2 and to vertex 4 with a distance of 3. Each line ends with -1. The given distances are all natural numbers not exceeding 10,000.

Output

Print the diameter of the tree on the first line.

Example Input

5
1 3 2 -1
2 4 4 -1
3 1 2 4 3 -1
4 2 4 3 3 5 6 -1
5 4 6 -1

Example Output

11

Example source code

import sys

input = sys.stdin.readline

def read_input():
    num_vertices = int(input())
    graph = [[] for _ in range(num_vertices + 1)]

    for _ in range(num_vertices):
        line = list(map(int, input().split()))
        vertex = line[0]
        idx = 1
        while line[idx] != -1:
            connected_vertex, weight = line[idx], line[idx + 1]
            graph[vertex].append((connected_vertex, weight))
            idx += 2
    return num_vertices, graph

def dfs(graph, start_vertex):
    stack = [(start_vertex, 0)]
    distances = [-1] * len(graph)
    distances[start_vertex] = 0
    max_distance, max_vertex = 0, start_vertex

    while stack:
        vertex, accumulated_distance = stack.pop()
        for next_vertex, weight in graph[vertex]:
            if distances[next_vertex] == -1:
                next_distance = accumulated_distance + weight
                distances[next_vertex] = next_distance
                stack.append((next_vertex, next_distance))
                if next_distance > max_distance:
                    max_distance, max_vertex = next_distance, next_vertex

    return max_distance, max_vertex

def find_tree_diameter(num_vertices, graph):
    _, farthest_vertex = dfs(graph, 1)
    max_distance, _ = dfs(graph, farthest_vertex)
    return max_distance

if __name__ == "__main__":
    num_vertices, graph = read_input()
    sys.stdout.write(str(find_tree_diameter(num_vertices, graph)) + '\n')

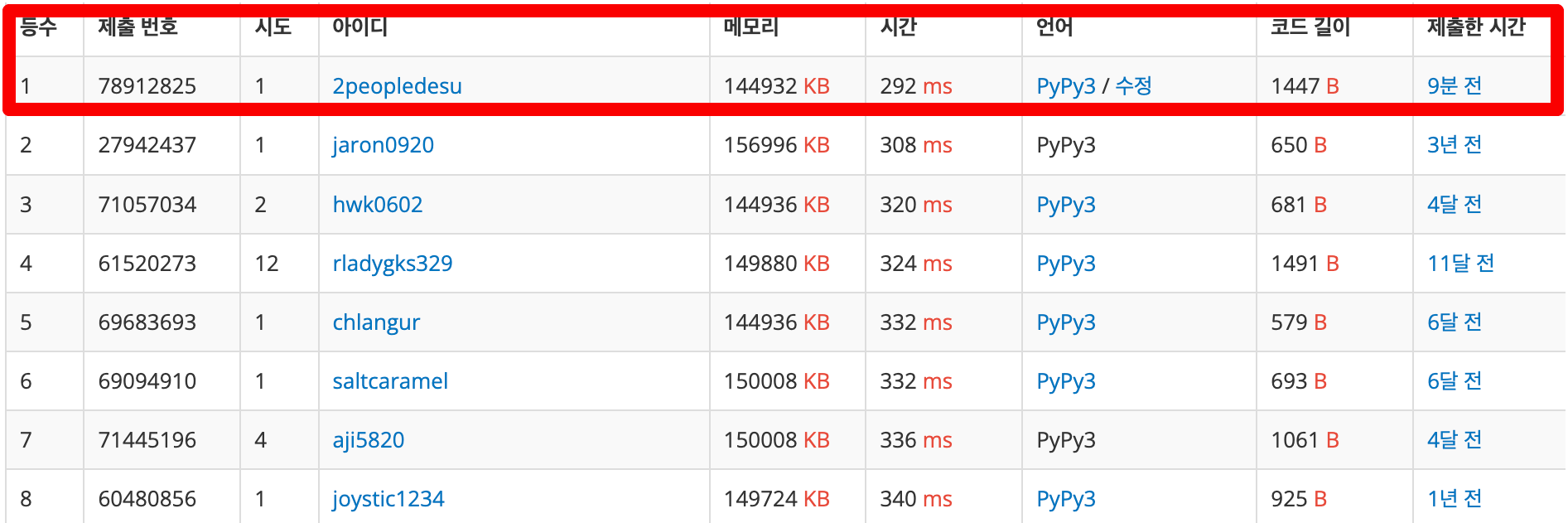
I achieved first place in the Python category on an algorithm site using the above code.