Definition

Dijkstra's Algorithm is designed to find the shortest path from a specific starting point to all other vertices in a graph.
For instance, if there are 5 vertices and we start from vertex 1, the algorithm will determine the shortest paths from vertex 1 to vertices 2 for through 5. Suppose we know the shortest distance to a point A, even though we don't know distances to other points.
If we can reach other points via A, we can estimate the distance to a specific point as the distance to A plus distance from A to that specific point. Dijkstra's algorithm is based on this idea.

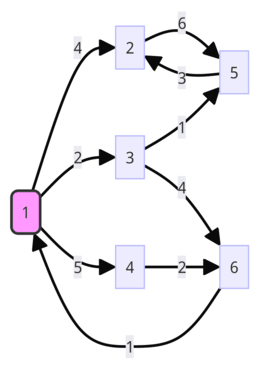
Let's assume we are calculating the shortest distances to each point starting from point 5. In Dijkstra's Algorithm, the distance array is initalized to a very large value(INF as sys.maxsize - 1) for all vertices, and only the starting point is set to 0. The reason for setting only the starting point to 0 is to clearly indicate that the shortest distance from the starting point to itself is 0.

In the Dijkstra's algorithm, we repeatedly select the minimum value from the distance array (dist). To effectively continue finding the minimum value in such cases, it is said that we should use a priority queue. Therefore, right from the start, we insert all vertices from 1 to 6 into the priority queue so that we can select the minimum value among the distances.

def dijkstra(graph, source):
    # Graph and starting point information are given
    Q = []  # Creating a priority queue
    dist = {}  # Distance dictionary
    
    # For all nodes in the graph
    for v in graph:
        dist[v] = float('inf')  # Set all initial values to a very large value
        Q.append(v)  # Insert each node into the priority queue
    dist[source] = 0  # Initialize the dist value for the start point to 0

    # While the priority queue is not empty
    while Q:
        # Select the node with the smallest dist value from the priority queue
        u = min(Q, key=lambda vertex: dist[vertex])
        Q.remove(u)  # Remove the node from the priority queue
        
        # For all nodes connected to node u
        for v in graph[u]:
            alt = dist[u] + graph[u][v]  # Calculate the sum of the current dist value and the edge weight
            # If the calculated value is smaller than the existing dist value
            if alt < dist[v]:
                dist[v] = alt  # Update the dist value to the calculated value
                
    return dist

When there are negative weights, Dijkstra's algorithm cannot absolutely determine the shortest distance.